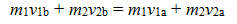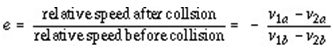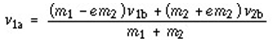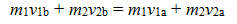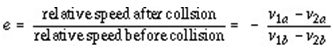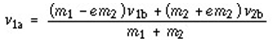The impact between bat and ball is a collision between two objects, and in its simplest analysis the collision may be taken to occur in one-dimension. In reality most collisions between bat and ball (especially the ones I am able to make) are glancing collisions which require a two-dimensional analysis. 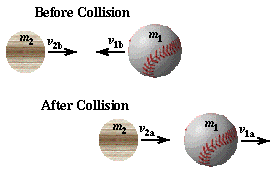It turns out, in fact, that a glancing blow is necessary to impart spin to the ball which allows it to travel farther.^[5] Maybe I'll write about this more interesting, but more difficult problem later, but for right now I'll keep things simple and look at the collision in one-dimension only. The ball, m₁, and bat, m₂, both have initial velocities before the collision (subscript "b"), with the ball's velocity being negative. After the collision (subscript "a") both bat and ball have positive velocities. The before and after velocities and the masses of bat and ball may be related to each other through the physical relationship known as the conservation of linear momentum. Linear momentum is the product of the mass and velocity of an object, p=mv. If the net force acting on a system of objects is zero then the total momentum of the system is constant. While the bat and ball are in contact the player is exerting a force on the bat; the force needed to swing the bat. So, in a completely correct analysis, momentum is not constant because of this force exerted by the player swinging the bat. However, the force on the bat by the player is very much smaller than the forces between bat and ball during the collision, and the contact time between ball and bat is very short (less than 1 millisecond). This allows us to ignore the force on the bat by the player during the collision between ball and bat without significantly affecting our results. If we ignore the force by the player on the bat, we can express the conservation of linear momentum by setting the total momentum before the collision equal to the total momentum after the collision.

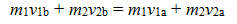
Usually when a student encounters the conservation of momentum in a physics course the masses of both objects are given, along with the initial velocities before the collision. A typical homework or quiz question would be to determine the final velocities of the two objects after the collision. When one is searching for two unknown quantities one must have two equations. So, we need more than just the conservation of momentum. For our student in a physics course this second equation is usually the conservation of energy. The conservation of energy relates the change in kinetic energy (associated with motion), the change in potential energy (associated with springs and position), and any work done by nonconservative forces (like friction) which act on the system. The change in kinetic energy includes information about the velocities of the ball and bat before and after the collision. During the collision the ball undergoes a significant amount of compression, and damping forces convert much of the ball's initial kinetic energy into heat. The change in potential energy and work done by friction describe how much of the initial energy is lost during compression of the bat and ball. The manner in which these energies are related during the bat-ball collision is rather complicated. However, the effective relationship between the elastic properties of the ball and the relative velocities of bat and ball may be summarized in terms of the coefficient of restitution, (e)

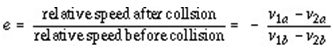
The coefficient of restitution of a baseball or softball decreases with increasing incoming ball speed (v_1b). Modern baseballs are manufactured to have a coefficient of restitution of 0.55 for a 90mph pitch speed, while softballs are manufactured to have e=0.44 for pitch speeds of 60 mph. Assuming a constant pitch speed, we can combine two equations above and do a little algebra to solve for the velocity of the baseball after the collision:

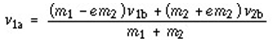
This equation tells us how the batted ball velocity (v_1a)depends on the mass of the ball (m₁) and bat (m₂), the elasticity of the ball (e), the pitched ball speed (v_1b) and the bat swing speed (v_2b). The properties of the ball may be treated as constants since they don't change during a turn at bat. The hitter has no control over the pitched ball speed, and while it may vary considerably from pitch to pitch we'll assume that it is a constant. The only two remaining variables which determine the final velocity of the ball are the mass of the bat, m₂ and the initial speed of the bat, v_2b. If we know these two parameters, we can predict the batted ball speed. As we will see, however, the problem is complicated somewhat by the fact that the speed with which a player can swing a bat depends on the weight of the bat.